Website of R. Harald Baayen
Professor of Quantitative Linguistics
ERC-SUBLIMINAL project, DFG-Cwic project
Research Interests
I am interested in words: their internal structure, their meaning, their distributional properties, how they are used in different speech communities and registers, and how they are processed in language comprehension and speech production. There are four main themes in my research:
Morphological Productivity
The number of words that can be described with a word formation rule varies substantially. For instance, in English, the number of words that end in the suffix -th (e.g., warmth) is quite small, whereas there are thousands of words ending in the suffix -ness (e.g., goodness). The term 'morphological productivity' is generally used informally to refer to the number of words in use in a language community that a rule describes.
For a proper understanding of the intriguing phenomenon of morphological productivity, I believe it is crucial to distinguish between (a) language-internal, structural factors, (b) processing factors, and (c) social and stylistic factors. (For a short review, see my contribution to the HSK handbook of corpus linguistics . Formal linguists tend to focus on (a), psychologists on (b), and neither like to think about (c). Sociologists and anthropologists would probably only be interested in (c).
In order to make the rather fuzzy notion of quantity that is part of the concept of morphological productivity more precise, I have developed several quantitative measures based on conditional probabilities for assessing productivity (Baayen 1992, 1993, Yearbook of Morphology). These measures assess the outcome of all three kinds of factors mentioned above, and provide an objective starting point for interpretation given for the kind of materials sampled in the corpora from which they are calculated.
In a paper in Language from 1996, co-authored with Antoinette Renouf (pdf), we show how these productivity measures shed light on the role of structural factors. Hay (2003, Causes and Consequences of Word Structure, Routledge) documented the importance of phonological processing factors, which are addressed for a large sample of English affixes in Hay and Baayen (2002, Yearbook of Morphology, (pdf) as well as in Hay and Baayen (2003) in the Italian Journal of Linguistics (pdf).
Social and stylistic factors seem to be at least equally important as the structural factors determining productivity, see, e.g., Baayen, 1994, in the Journal of Quantitative Linguistics (pdf), the study of Plag et al. (1999) in English Language and Linguistics (pdf), and for register variation and productivity, Baayen and Neijt (1997) in Linguistics (pdf).
Hay and Plag (2004, Natural Language and Linguistic Theory) presented evidence that affix ordering in English is constrained by processing complexity. Complexity-based ordering theory holds that an affix that is more difficult to parse should occur closer to the stem than an affix this is easier to parse. (This result is related to the productivity paradox observed by Krott et al., 1999, published in Linguistics (pdf), according to which words with less productive affixes are more likely to feed further word formation.)
More recently, however, a study surveying a broader range of affixes, co-authored with Ingo Plag and published in Language in 2009 (pdf) documented an inverse U-shaped functional relation between suffix ordering and processing costs in the visual lexical decision and word naming tasks. Words with the least productive suffixed revealed, on average, the shortest latencies, and words with intermediate productivity the longest latencies. The most productive suffixes showed a small processing advantage compared to intermediately productive suffixes. This pattern of results may indicate a trade-off between storage and computation, with the costs of computation overriding the costs of storage only for the most productive suffixes.
In terms of graph theory, complexity-based ordering theory holds that the directed graph of English suffixes is acyclic. In practice, one typically observes a small percentage (10% or less) of affix orders violating acyclicity. In a recent study, The directed compound graph of English An exploration of lexical connectivity and its processing consequences (pdf), I showed that constituent order for two-constituent English compounds is also largely acyclic, with a similar violation rate as observed for affixes. The rank ordering for compounds, however, is not predictive at all for lexical processing costs. This suggests that acyclicity is not necessarily the result of complexity-based constraints. What emerged as important for predicting processing costs in this study are graph-theoretical concepts such as membership of the strongly connected component of the compound graph, and the shortest path length of the head to the modifier.
Morphological Processing
How do we understand and produce morphologically complex words such as hands and boathouse? The classical answer to this question is that we would use simple morphological rules, such as the rule adding an s to form the plural, or the rule allowing speakers to form compounds from nouns. I have always been uncomfortable with this answer, as so much of what makes language such a wonderful vehicle for literature and poetry is the presence of all kinds of subtle (and sometimes not so subtle) irregularities. Often, a 'rule' captures a main trend in a field in which several probabilistic forces are at work. Furthermore, an appeal to rules raises the question of how these supposed rules would work, would be learned, and would be implemented in the brain.
Nevertheless, morphological rules enjoy tremendous popularity in formal linguistics, which tends to view the lexicon as the repository of the unpredictable. The dominant metaphor is that of the lexicon as a calculus, a set of elementary symbols and rules for combining those symbols into well-formed expressions. The lexicon would then be very similar to a pocket calculator. Just as a calculator evaluates expressions such as 3+5 (returning 8), a morphological rule would evaluate hands as the plural of hand. Moreover, just as a calculator does not have in memory that 3+5 is equal to eight, irrespective of how often we ask it to calculate 3+5 for us, the mental lexicon (the structures in the brain subserving memory for words and rules) would not have a memory trace for the word hands. Irrespective of how often we would encounter the word hands, we would forget having seen, heard, or said the plural form. All we would remember is having used the word hand.
The problem with this theory is that the frequency with which a word is encountered in speech and writing co-determines the fine acoustic details with which it is pronounced, as well as how quickly we can understand it. For instance, Baayen, Dijkstra, and Schreuder published a study in the Journal of Memory and Language in 1997 (pdf) indicating that frequent plurals such as hands are read more quickly than infrequent plurals such as noses. Baayen, McQueen, Dijkstra, and Schreuder, 2003 (pdf) later reported the same pattern of results for auditory comprehension. Further discussion of this issue can be found in a book chapter co-authored with Rob Schreuder, Nivja de Jong, and Andrea Krott from 2002 (pdf). Even for speech production, there is evidence that the frequencies with which singulars and plurals are used co-determine the speed with which we pronounce nouns (Baayen, Levelt, Schreuder, Ernestus, 2008, (pdf)).
In recent studies using eye-tracking methodology, first fixation durations were shorter for more frequent compounds, even though the whole compound had not yet been scanned visually (see Kuperman, Schreuder, Betram and Baayen, JEP:HPP, 2009 for English, (pdf) and Miwa, Libben, Dijkstra and Baayen (submitted, available on request) for Japanese). These early whole-word frequency effects are incompatible with pocket calculator theories, and with any theory positing that reading critically depends on an initial decomposition of the visual input into its constituents.
Lexical memory also turns out to be highly sensitive to the fine details of the acoustic signal and the probability distributions of these details, see, for instance, Kemps, Ernestus, Schreuder, and Baayen, Memory and Cognition, 2005 (pdf). Work by Mark Pluymaekers, Mirjam Ernestus, and Victor Kuperman in the Journal of the Acoustical Society of America ((pdf) and (pdf)) indicates, furthermore, that the degree of affix reduction and assimilation in complex words correlates with frequency of use. Apparently, a word's specific frequency co-determines the fine details of its phonetic realization.
In summary, the metaphor of the brain working essentially as a pocket calculator is not very attractive in the light of what we now know about the sensitivity of our memories to frequency of use and to phonetic detail of individual words, even if they are completely regular.
Given that our brains have detailed memories of regular complex words, it seems promising to view the mental lexicon as a large instance base of forms that serve as exemplars for analogical generalization. Given pairs such as hand/hands, dot/dots and pen/pens, the plural of cup must be cups. Exemplar theories typically assume that the memory capacity of the brain is so vast that individual forms are stored in memory, even when they are regular. Exemplar theories can therefore easily accommodate the fact that regular complex words can have specific acoustic properties, and that their frequency of occurrence co-determines lexical processing. They also offer the advantage of being easy to implement computationally. In other words, in exemplar-based approaches to the lexicon, the lexicon is seen as a highly redundant, exquisite memory memory system, in which 'analogical rules' become, possibly highly local, generalizations over stored exemplars. Analogy (a word detested by linguists believing in calculator-like rules) can be formalized using well-validated techniques in statistics and machine learning. Techniques that I find especially insightful and useful are Royal Skousen's Analogical Modeling of Language (AML), and the Tilburg Memory Based Learner TiMBL developed by Walter Daeleman and Antal van den Bosch.
These statistical and machine learning techniques turn out to work very well for phenomena that resist description in terms of rules, but where native speakers nevertheless have very clear intuitions about what the appropriate forms are. Krott, Schreuder and Baayen (Linguistics, 1999, (pdf)) used TiMBL's nearest neighbor algorithm to solve the riddle of Dutch interfixes, Ernestus and Baayen studied several algorithms for understanding the subtle probabilistic aspects of the phenomenon of final devoicing in Dutch ((pdf) and (pdf)). Ingo Plag and his colleagues have used TiMBL to clarify the details of stress placement in English (see Plag et al. in Corpus Linguistics and Linguistic Theory 2007 and in Language, 2008).
Especially for compounds, a coherent pattern emerges for how probabilistic rules may work in languages such as English and Dutch. For compound stress, for interfixes, and, as shown by Cristina Gagne, for the interpretation of the semantic relation between modifier and head in a compound (see Gagne and Shoben, JEP:LMC 1997 and subsequent work), the probability distribution of the possible choices given the modifier appears to be the key predictor.
The importance of words' constituents as a domains of probabilistic generalization ties in well with results obtained on the morphological family size effect. Simple words that occur as a constituent in many other words (in English, words such as mind, eye, fire) are responded to more quickly in reading tasks than words that occur in only a few other words (e.g., scythe, balm). This effect, first observed for Dutch ((pdf), (pdf), (pdf)) has been replicated for English and typologically unrelated languages such as Hebrew, and Finnish ((pdf), (pdf)). Words with many paradigmatic connections to other words are processed faster, and these other words in turn constitute exemplar sets informing analogical generalization.
Although exemplar-based approaches to lexical processing are computationally very attractive, they come with their own share of problems. One question concerns the redundancy that comes with storing many very similar exemplars, a second question addresses the vast numbers of exemplars that may need to be stored. With respect to the first question, it is worth noting that any workable and working exemplar-based system, such as TiMBL, implements smart storage algorithms to alleviate the problem of looking up a particular exemplar in a very large instance base of exemplars. In other words, in machine learning approaches, some form of data compression tends to be part of the computational enterprise.
The second question, however, is more difficult to waive aside. Until recently, I thought that the number of different word forms in languages such as Dutch and English is so small, for an average educated adult native speaker well below 100.000, that the vast storage capacity of the human brain should easily accommodate such numbers of exemplars. However, recently several labs have reported frequency effects for sequences of words. For instance, http://www.ncilab.ca/people Antoine Tremblay studied sequences of four words in an immediate recall task and observed frequency effects in the evoked response potentials measured at the scalp (pdf). Crucially, these frequency effects (with frequency effects for subsequences of words controlled for) emerged not only for full phrases (such as on the large table) but also for partial phrases such (such as the president of the). There are hundreds of millions of different sequences of word pairs, word triplest, quadruplets, etc. It is, of course, possible that the brain does store all these hundreds of millions of exemplars, but I find this possibility unlikely. This problem of an exponential explosion of exemplars does not occur only when we move from word formation into syntax, it also occurs when we move into the auditory domain and consider acoustic exemplars for words. Even the same speaker will never say a given word in exactly the same way twice. Assuming exemplars for the acoustic exemplars of the words again amounts to assuming that staggering numbers of exemplars would be stored in memory (see, e.g., Ernestus and Baayen (2011) (pdf) for discussion).
There are several altenatives to exemplar theory. A first option is to pursue the classic position in generative linguistics, and to derive abstract rules from experience, obviating the need for individual exemplars. Whereas exemplar models such as TiMBL can be characterized aslazy learning, with analogical generalization operating at run time over an instance base of exemplars, greedy learning is characteristic of rule systems such as the Minimum Generalization Learner (MGL) of Albright and Hayes (Cognition, 2003), that derive large sets of complex symbolic rules from the input. Such systems are highly economical in memory, but this approach comes with its own price. First, I find the complexity of the derived systems of rules unattractive from a cognitive perspective. Second, once trained, the system works but can't learn: it ends up functioning like a sophisticated pocket calculator. Third, such approaches leave unexplained the existence of frequency and family size effects for (regular) complex words. Interestingly, Emmanuel Keuleers, in his Antwerpen 2008 doctoral dissertation, points out that from a computational perspective, the MGL and a nearest neighbor exemplar-based model are equivalent, the key difference being that the point at which the exemplars are evaluated: during learning for MGL, at runtime for the exemplar model.
A second alternative is to turn to connectionist modeling. Artificial neural networks (ANNs, see, e.g., the seminal study of Rumelhart and McClelland, 1986) offer many advantages. They are powerful statistical pattern associators, they implement a form of data compression, they can be lesioned for modeling language deficits, they are not restricted to discrete (or discretisized) input, etc. On the downside, it is unclear to what extent current connectionist models can handle the symbolic aspects of language (see, e.g., Levelt, 1991, Sprache und Kognition), and the performance of ANNs is often not straightforwardly interpretable. Although the metaphor of neural networks is appealing, the connectionist models that I am aware of make use of training algorithms that are mathematically sophisticated but biologically implausible. Nevertheless, connectionist models can provide surprisingly good fits to observed data on lexical processing. I have had the pleasure of working with Fermin Moscoso del Prado Martin for a number of years, and his connectionist models (see (pdf), and (pdf)) capture frequency effects, family size effects, as well as important linguistic generalizations.
Recently, in collaboration with Peter Milin, Peter Hendrix and Marco Marelli, I have been exploring an approach to morphological processing based on discriminative learning as defined by the Rescorla-Wagner equations. These equations specify how the strength of a cue to a given outcome changes over time as a function of how valid that cue is for that outcome. Ramscar, Yarlett, Dye, Denny and Thorpe (2010, Cognitive Science) have recently shown that the Rescorla-Wagner equations make excellent predictions for language acquisition. Following their lead, we have been examining the potential of these equations for morphological processing. The basic intuition is the following. Scrabble players know that the letter pair qa can be used for the legal scrabble words qaid, qat and qanat. The cue validity of qa for these words is quite high, whereas the cue validity of just the a for these words is very low - there are lots of more common words that have an a in them (apple, a, and, can, ...). Might it be the case that many of the morphological effects in lexical processing arise due to the cue strengths of orthographic information (provided by letters and letter pairs) to word meanings?
To address this question, we have made use of the equilibrium equations developed by Danks (Journal of Mathematical Psychology, 2003), which make it possible to estimate the weights from the cues (letters and letter pairs) to the outcomes (word meanings) from corpus-derived co-occurrence matrices, in our case co-occurrence matrices derived from 11,172,554 two and three-word phrases (comprising in all 26,441,155 word tokens) taken from the British National Corpus. The activation of a meaning was obtained by summing the weights from the active letters and letter pairs to that meaning. Response latencies were modeled as inversely proportional to this activation, and log-transformed to remove for statistical analysis the skew from the resulting distribution of simulated reaction times. We refer to this model as the Naive Discriminative Reader, where 'naive' refers to the fact that the weights to a given outcome are estimated independently of the weights to other other outcomes. The model is thus naive in the naive Bayes sense.
It turns out that this very simple, a-morphous, architecture captures a wide range of effects documented for lexical processing, including frequency effects, morphological family size effects, and relative entropy effects. For monomorphemic words, the Naive Discriminative Reader provides excellent predictions already without any free parameters. For morphologically complex words, good prediction accuracy requires a few free parameters. For instance, for compounds, it turns out that the meaning of the head noun is less important than the meaning of the modifier (which is read first). The model captures frequency effects for complex words, without there being representations for complex words in the model. The model also predicts phrasal frequency effects (Baayen and Hendrix 2011 (pdf) ), again without phrases receiving their own representations in the model. When used as a classifier for predicting the dative alternation, the model performs as well as a generalized linear mixed-effects model and as a support vector machine (pdf) .
The naive discriminative reader model differs from both subsymbolic and interactive activation connectionist models. The model does not belong to the class of subsymbolic models, as the representations for letters, letter pairs, and meanings are all straightforward symbolic representations. There are also no hidden layers, and no backpropagation. It is also not an interactive activation model, as there is only one forward pass of activation. Furthermore, its weights are not set by hand, but are derived from corpus input. In addition, it is extremely parsimoneous in the number of representations required, especially compared to interactive activation models incorporating representations for n-grams. Thus far, the results we have obtained with this new approach are encouraging. To our knowledge, there are currently no other implemented computational models for morphological processing available that correctly predict the range of morphological phenomena handled well by the naive discriminative reader. It will be interesting and informative to discover where its predictions break down.
Language Variation
My interest in stylometry was sparked by the seminal work of John Burrows, who documented stylistic, regional, and authorial differences by means of principal components analyses applied to the relative frequencies of the highest-frequency function words in literary texts. Burrows' research inspired a study published in the Journal of Quantitative Linguistics entitled Derivational Productivity and Text Typology (pdf), which explored the potential of a productivity measure for distinguishing different text types. Baayen, Tweedie and Van Halteren (1996, Literary and Linguistic Computing) compared function words with syntactic tags in an authorship identification study. Baayen, Van Halteren, Neijt and Tweedie (2002, Proceedings JADT, (pdf)) and Van Halteren, Baayen, Tweedie, Haverkort, and Neijt (JQL, 2005, (pdf) showed that in a controlled experiment, the writings of 8 students of Dutch language and literature at the university of Nijmegen could be correctly attributed to a remarkable degree (80% to 95% correct attributions), which was reanalyzed with Patrick Juola in a CHUM paper entitled A Controlled-Corpus Experiment in Authorship Identification by Cross-Entropy (pdf). For a study on the socio-stylistic stratification of the Dutch suffix -lijk in speech and writing, see Keune et al. (2006, (pdf)), and for the application of mixed effects modeling in sociolinguistic studies of language variation, see Tagliamonte and Baayen (2012), (pdf)). I am also interested in individual differences between speakers/writers in experimental tasks. For a study suggesting individual differences between speakers with respect to storage and computation of complex words, see my paper with Petar Milin (pdf). For register variation in morphological productivity, see, e.g., Plag et al. (1999) (pdf) in English Language and Linguistics.
Statistical Analysis of Language Data
My book on word frequency distributions (Kluwer, 2001) gives an overview of statistical models for word frequency distributions. Stefan Evert developed the LNRE extension of the Zipf-Mandelbrot model (Evert, 2004, JADT proceedings), which provides a flexible and often much more robust extension of the line of work presented in my book.
I have found R to be a great open-source tool for data analysis. My book with Cambridge University Press, Analyzing Linguistic Data: A practical introduction to Statistics using R, provides an introduction to R for linguists and psycholinguists. An older version of this book, with various typos and small errors, is available (see my list of publications for a link). The data sets and convenience functions used in this textbook are available in the 'languageR' package that is available from the CRAN archives. Recent versions of this package have some added functionality that is not documented in my book, such as a function for plotting the partial effects of mixed-effects regression models (plotLMER.fnc) and a function for explorin g autocorrelational structure in psycholinguistic experiments (acf.fnc).
Mixed effects modeling is a beautiful technique for understanding the structure of data sets with both fixed and random effec ts as typically obtained in (psycho)linguistic experiments. My favorite reference for nested random effects is Pinheiro and Bates (2000, Springer). For data sets with crossed fixed and random effects, the lme4 package of Douglas Bates provides a flexible tool kit for R. A paper co-authored with Doug Davidson and Douglas Bates in JML, Mixed-effects modeling with crossed random effect s for subjects and items (pdf) and chapter 7 of my introductory textbook provide various examples of its use. A highly recommended more technical book on mixed effects modeling that provides detailed examples of crossed random effects for subjects and item s is Julian J. Faraway (2006), Extending Linear Models with R: Generalized Linear, Mixed Effects and Nonparametric Regression Models, Chapman and Hall. Practical studies discussing methodological aspects of mixed effects modeling that I was involved in are Capturing Correlational Structure in Russian Paradigms: a Case Study in Logistic Mixed-Effects Modeling (with Laura Janda and Tore Nesset) (pdf) ,Analyzing Reaction Times (with Petar Milin) (pdf), Models, Forests and Trees of York English: Was/Were Variation as a Case Study for Statistical Practice, with Sali Tagliamonte (pdf), and Corpus Linguistics and Naive Discriminative Learning (pdf). A general methodological paper (pdf) illustrates by means of some simulation studies the disadvantages of using factorial designs, still highly popular in psycholinguistics, for investigations for which regression designs are more appropriate.
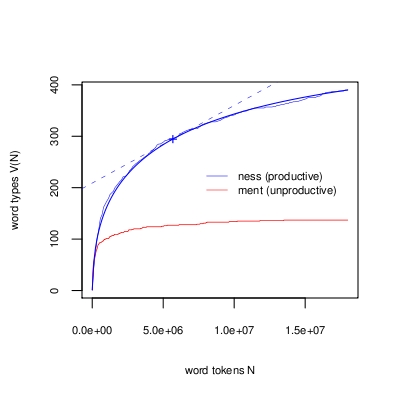
The probability of encountering a new, previously unseen word type in a text after N word tokens have been read is given by the slope of the tangent to the curve at the point (N, V(N)). This slope (a result due to Turing), is equal to the number of word types occurring exactly once in the first N tokens, divided by N. The curves in the above figure show how the number of different words ending in ness keep increasing when reading through an 18 million word corpus, while the number of different words ending in ment quickly reaches a horizontal asymptote, indicating that the probability of observing new formations with this suffix is zero. Baayen (1992) introduces this approach to measuring productivity in further detail.
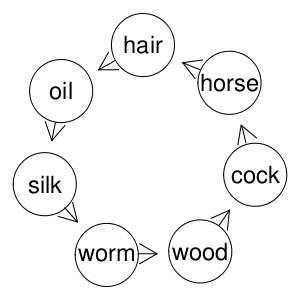
A cycle in the English compound graph: (woodcock, cockhorse, horsehair, hair oil, oil-silk, silkworm, wormwood). Each modifier is also a head, and each head is also a modifier.
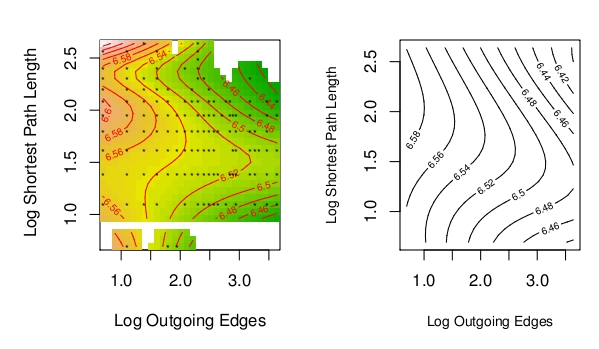
Cost surface for reading aloud of compounds, as a function of the number of outgoing edges for the modifier and the shortest path length from the head to the modifier. The observed surface (left) is well approximated by a theoretical surface (right) derived from the hypothesis that activation traveling from the head through the network to the modifier interferes most strongly when the path is not too long and not too short. Very short paths (houseboat/boathouse) don't interfere due to strong support from the visual input, very long paths don't interfere due to activation decay with each step through the cycle. Further details are available in Baayen (2010)
The calculus of formal languages do not provide a useful metaphor for understanding how the brain deals with words. The brain is not a pocket calculator that never remembers what it computes.
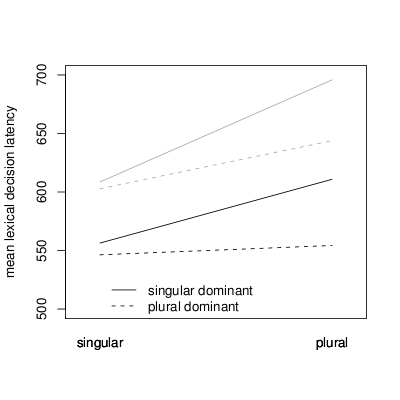
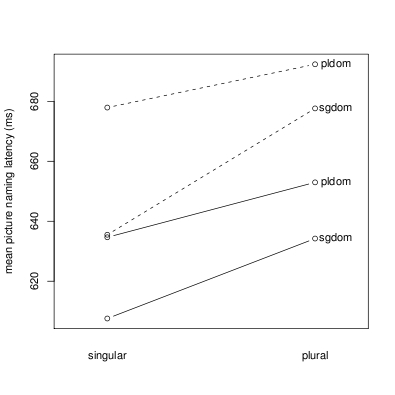
Frequency dominance effects in reading and listening (top) differ from those in speaking (bottom). A singular dominant noun is a noun for which the singular is more frequent than the plural (e.g., nose). A plural dominant noun is characterized by a plural that is more frequent than its singular (e.g., hands). In reading and listening, a plural-dominant plural is understood more quickly than a singular dominant plural matched for stem frequency, for both high-frequency and low-frequency nouns. In speech, surprisingly, both plurals and singulars require more time to pronounce when the plural is dominant. Baayen, Levelt, Schreuder, and Ernestus (2008) show that this delay in production is due to the greater information load (entropy) of the inflectional paradigms of plural-dominant nouns.
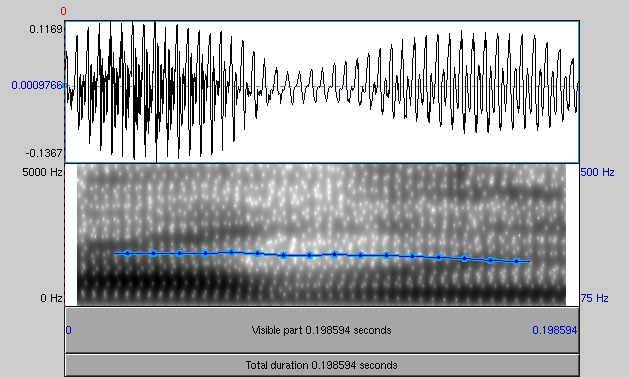
Complex words that are used frequently tend to be shortened considerably in speech, to such an extent that out of context the word cannot be recognized. In context, the brain restores the acoustic signal to its canonical form. Kemps, Ernestus, Schreuder and Baayen (2004) (pdf) demonstrated this restoration effect for Dutch suffixed words. For English, the following example illustrates the phenomenen. First listen to this audio file, which plays a common high-frequency English word. Heard by itself, the word makes no sense at all. Now listen to this word in an audio file that also plays the sentential context. The sentence and the reduced word are spelled out here. A leading specialist on acoustic reduction is Mirjam Ernestus.
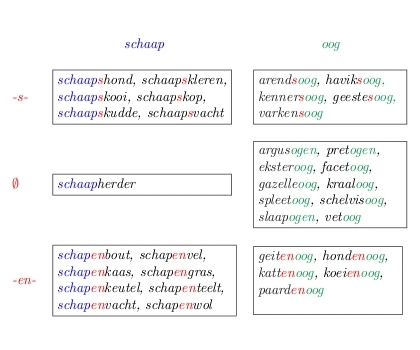
Analogical selection of an interfix for the Dutch compound schapenoog is based primarily on the distribution of interfixes in the set of compounds sharing the modifier schaap. As in this set en is the interfix that is attested most often, this is the preferred interfix for this compound. See Krott, Schreuder and Baayen (1999) for further discussion. The assignment of stress in English compounds and the interpretation of the semantic relation between modifier and head is based on exactly the same principle, with the modifier as the most important domain of probability-driven generalization.
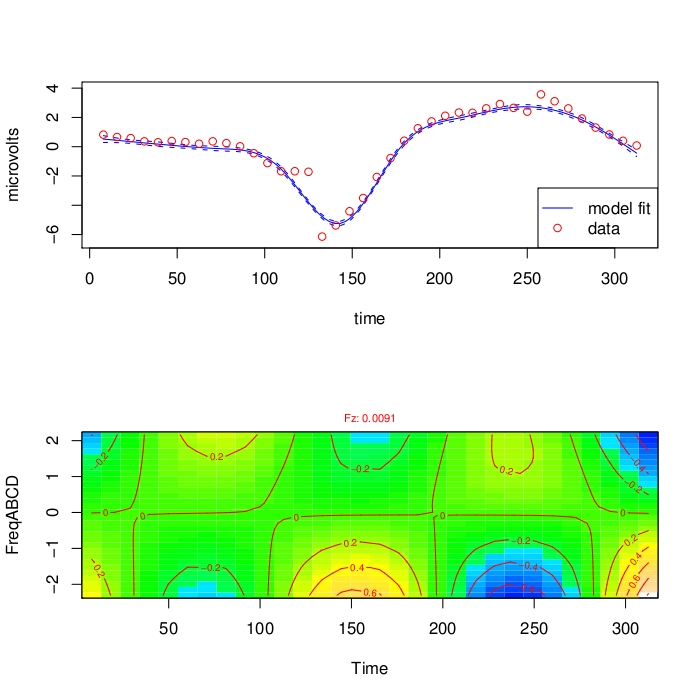
The frequency of a four-word sequence (n-gram) modulates the evoked response potential 150 milliseconds post stimulus onset in an immediate recall task at electrode Fz. The top panel shows the main trend, with the standard negativity around 150 ms. The bottom panel shows how this general trend is modulated by the frequency of the four-word phrase (FreqABCD on the vertical axis). For the lower n-gram frequencies, higher-amplitude theta oscillations are present. Tremblay and Baayen (2010) provide further details.
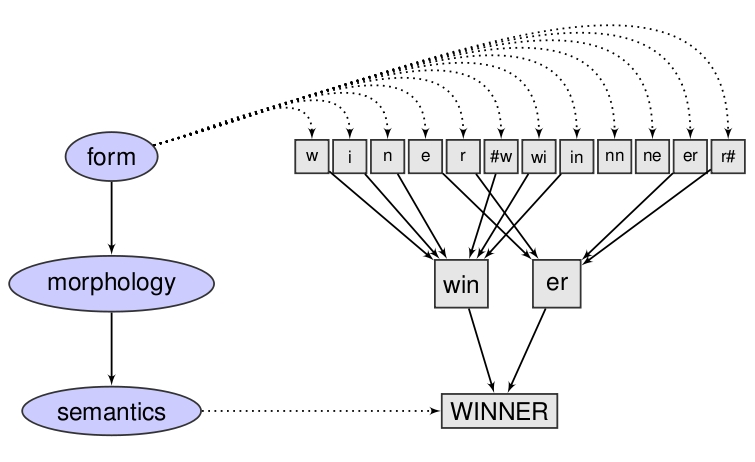
A popular model in the psychology of reading is that orthographic morphemes (e.g., win and er for winner) mediate access from the orthographic level to word meanings. This theory has, as far as I know, never been implemented in a computational model.
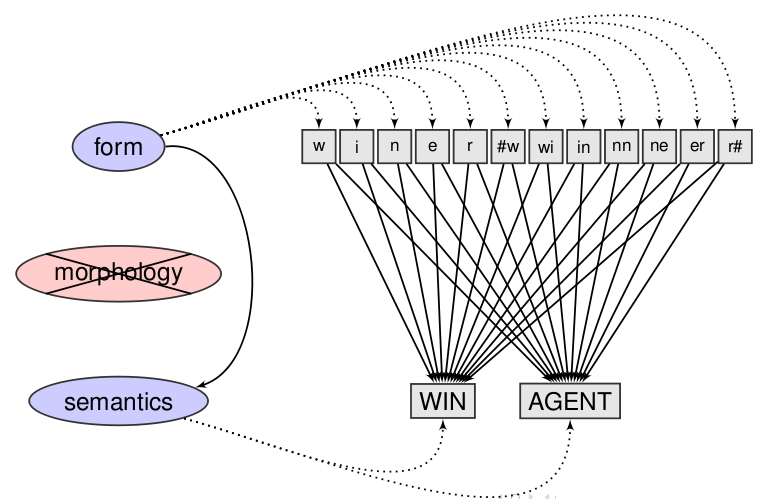
In the naive discriminative reader model (computationally implemented in R in the package ndl), there is no separate morpho-orthographic representational layer. Orthographic representations for letters and letter pairs are connected directly to basic meanings such as WIN and AGENT. The weights on the links are estimated from the co-occurrence matrix of the cues on one hand, and the co-occurrence matrix of outcomes and cues on the other, using the equilibrium equations for the Rescorla-Wagner equations developed in Danks (Journal of Mathematical Psychology, 2003). The estimates are optimal in the least-squares sense.
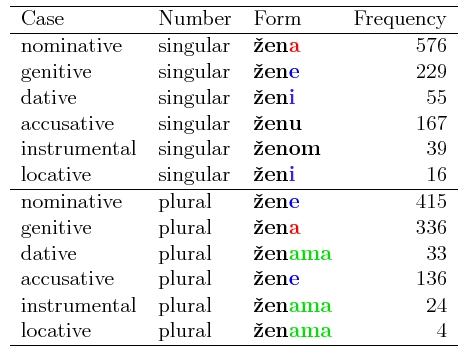
Why no morphemes? Many morphologists (e.g., Matthews, Anderson, Blevins) have argued that affixes are not are not signs in the Saussurian sense. For instance, the Serbian case ending a in žena (woman) represents either NOMINATIVE and SINGULAR, or PLURAL and GENITIVE. Normal signs such as tree may have various shades of meaning (such as 'any perennial woody plant of considerable size', 'a piece of timber', 'a cross', 'gallows'), but these different shades of meaning are usually not intended simultaneously.
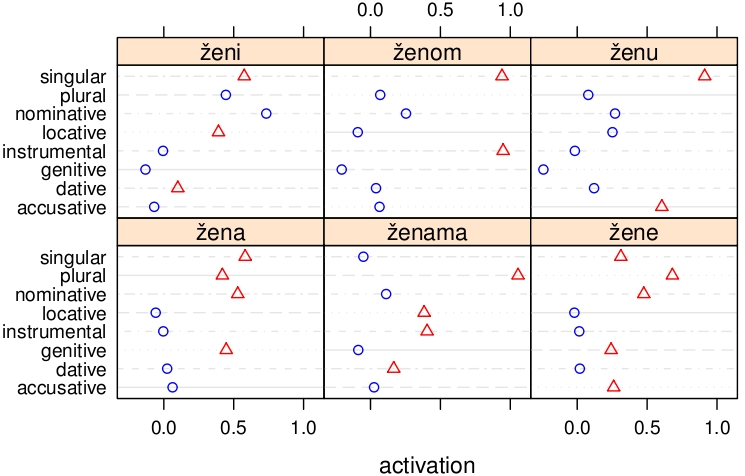
The naive discriminative predicts activation of all grammatical meanings associated with a case ending, depending on the frequencies with which these meanings are used, on how these meanings are used across the other words in the same inflectional class (cf. Milin et al., JML, 2009), and on their use in other inflectional classes. The red triangles indicate the activations predicted by the naive discriminative reading model for the correct meanings, the blue circles represent the activations of meanings that are incorrect. As hoped for, the red triangles tend to be to the right of the blue circles, indicating higher activation for correct meanings. For ženi, however, we have interference from the -i case ending expressing nominative plural in masculine nouns.
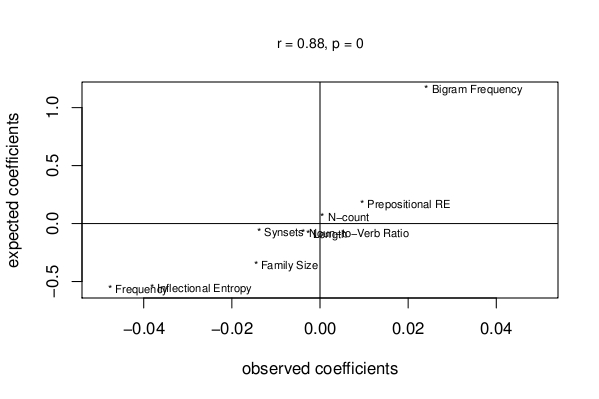
The coefficients of a regression model fitted to the observed reaction times to 1289 English monomorphemic words in visual lexical decision correlate well (r = 0.88) with the coefficients of the same regression model fitted to the simulated latencies predicted by the naive discriminative reader model. The model not only captures the effects of a wide range of predictors (from left to right, Word Frequency, Inflectional Entropy, Morphological Family Size, Number of Meanings, Word Length, Noun-Verb Ratio, N-count, Prepositional Relative Entropy, and Letter Bigram Frequency), but also correctly captures the relative magnitude of these effects.
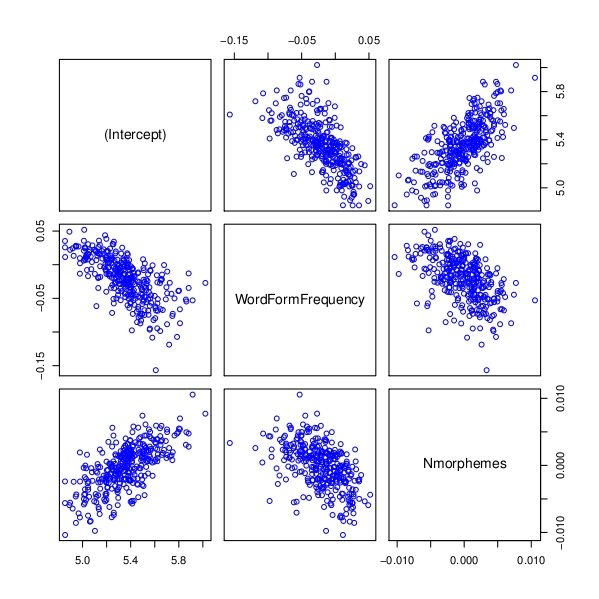
Scatterplot matrix for by-subject intercepts and slopes according to a mixed-effects regression model for self-paced reading of Dutch poetry. Slower readers have larger intercepts. For most participants, the slope for Word Form Frequency is negative: they read more frequent words faster, as expected. Participants are split with respect to how they process complex words. There are subjects who read complex words with more constituents more slowly, while other subjects read words faster if they contain more constituent (Nmorphemes). Interestingly, the slow readers are more likely to experience more facilitation from word frequency. Conversely, the slow readers dwell longer on a word, the more constituents it has. In addition, readers who read words that have more constituents fastest are also the readers who do not show facilitation from word frequency. Apparently, within the population of our informants, there is a trade-off between constituent-driven processing and memory-based whole-word processing. Most participants are balanced, but at the extremes we find both dedicated lumpers and avid splitters. Further details on this experiment can be found in Baayen and Milin (2011).
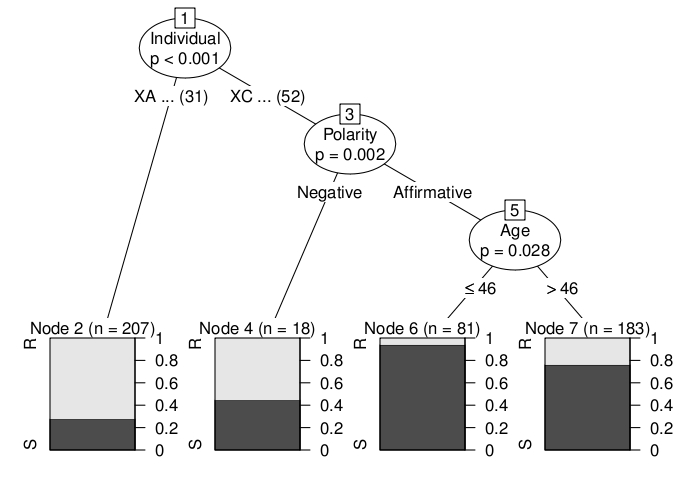
A conditional inference tree predicting the choice between was (S) and were (R) in sentences such as There wasn’t the major sort of bombings and stuff like that but there was orange men. You know there em was odd things going on. for York (UK) English. A random forest based on conditional inference trees (fitted with the party package for R) outperformed a generalized linear mixed model fitted to the same data in terms of prediction accuracy. See Tagliamonte and Baayen (2012) for further details.

